|
Students of physics and aerodynamics are taught that airplanes fly as a result of Bernoulli's principle, which says that if air speeds up the pressure is lowered. Thus a wing generates lift because the air goes faster over the top creating a region of low pressure, and thus lift. This explanation usually satisfies the curious and few challenge the conclusions. Some may wonder why the air goes faster over the top of the wing and this is where the popular explanation of lift falls apart.
In order to explain why the air goes faster over the top of the wing, many have resorted to the geometric argument that the distance the air must travel is directly related to its speed. The usual claim is that when the air separates at the leading edge, the part that goes over the top must converge at the trailing edge with the part that goes under the bottom. This is the so-called 'principle of equal transit times'.
As discussed by Gail Craig (Stop Abusing Bernoulli! How Airplanes Really Fly, Regenerative Press, Anderson, Indiana, 1997), let us assume that this argument were true. The average speeds of the air over and under the wing are easily determined because we can measure the distances and thus the speeds can be calculated. From Bernoulli's principle, we can then determine the pressure forces and thus lift. If we do a simple calculation we would find that in order to generate the required lift for a typical small airplane, the distance over the top of the wing must be about 50% longer than under the bottom. Figure 1 shows what such an airfoil would look like. Now, imagine what a Boeing 747 wing would have to look like!

Fig 1 Shape of wing predicted by principle of equal transit time
If we look at the wing of a typical small plane, which has a top surface that is 1.5 - 2.5% longer than the bottom, we discover that a Cessna 172 would have to fly at over 400 mph to generate enough lift. Clearly, something in this description of lift is flawed.
But, who says the separated air must meet at the trailing edge at the same time? Figure 2 shows the airflow over a wing in a simulated wind tunnel. In the simulation, colored smoke is introduced periodically. One can see that the air that goes over the top of the wing gets to the trailing edge considerably before the air that goes under the wing. In fact, close inspection shows that the air going under the wing is slowed down from the ‘free-stream’ velocity of the air. So much for the principle of equal transit times.
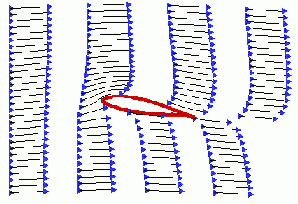
Fig 2 Simulation of the airflow over a wing in a wind tunnel, with colored ‘smoke’ to show the acceleration and deceleration of the air
The popular explanation also implies that inverted flight is impossible. It certainly does not address acrobatic airplanes, with symmetric wings (the top and bottom surfaces are the same shape), or how a wing adjusts for the great changes in load such as when pulling out of a dive or in a steep turn.
So, why has the popular explanation prevailed for so long? One answer is that the Bernoulli principle is easy to understand. There is nothing wrong with the Bernoulli principle, or with the statement that the air goes faster over the top of the wing. But, as the above discussion suggests, our understanding is not complete with this explanation. The problem is that we are missing a vital piece when we apply Bernoulli's principle. We can calculate the pressures around the wing if we know the speed of the air over and under the wing, but how do we determine the speed?
Another fundamental shortcoming of the popular explanation is that it ignores the work that is done. Lift requires power (which is work per time). As will be seen later, an understanding of power is key to the understanding of many of the interesting phenomena of lift.
MORE (Newton’s laws and lift)
|