aeRoman How airplanes fly 
Flag DE A Physical Description of Lift
MenuHomeAviationHumansOriginsScienceWeb LinksSite MapContact Almost everyone today has flown in an airplane. Many ask the simple question "what makes an airplane fly?" The answer one frequently gets is misleading and often just plain wrong. As an example, most descriptions of the physics of lift fixate on the shape of the wing (i.e. airfoil) as the key factor in understanding lift. The wings in these descriptions have a bulge on the top so that the air must travel farther over the top than under the wing. Yet we all know that wings fly quite well upside down where the shape of the wing is inverted. To cover for this paradox we sometimes see a description for inverted flight that is different than for normal flight. In reality the shape of the wing has little to do with how lift is generated and everything to do with efficiency in cruise and stall characteristics. Any description that relies on the shape of the wing is wrong.

Let us look at two examples of successful wings that clearly violate the descriptions that rely on the shape of the wing. The first example is a very old design. Figure 1 shows a photograph of the Curtis 1911 model D type IV pusher. Clearly the air travels the same distance over the top and the bottom of the wing. Yet this airplane flew and was the second airplane purchased by the US Army in 1911.

Curtis 1911 model D type IV pusher
Figure 1. Curtis 1911 model D type IV pusher

The second example of a wing that violates the idea that lift is dependent on the shape of the wing is of a very modern wing. Figure 2 shows the profile of the Whitcomb Supercritical Airfoil (NASA/Langley SC(2)-0714). This wing is basically flat on top with the curvature on the bottom. Though its shape may seem contrary to the popular view of the shape of wings, this airfoil is the foundation of the wings of modern airliners.

Whitcomb Supercritical Airfoil
Figure 2. Whitcomb Supercritical Airfoil

The emphasis on the wing shape in many explanations of lift is based on the Principle of Equal Transit Times. This assertion mistakenly states the air going around a wing must take the same length of time, whether going over or under, to get to the trailing edge. The argument goes that since the air goes farther over the top of the wing it has to go faster, and with Bernoulli’s principle we have lift. Knowing that equal transit times is not defendable the statement is often softened to say that since the air going over the top must go farther it must to faster. But, this is again just a variation on the idea of equal transit times. In reality, equal transit times holds only for a wing without lift. Figure 3 shows a simulation of the airflow around a wing with lift.

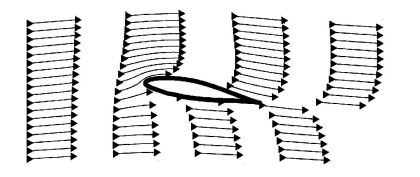
Air over a wing with lift
Figure 3. Air over a wing with lift

The Bernoulli equation is a statement of the conservation of energy. It is correct, but not applicable to the description of lift on a real wing. The wings of an 800,000 pound airplane are doing a great deal of work to keep the airplane in the air. They are adding a large amount of energy to the air. One of the requirements of the application of the Bernoulli principle is that no energy is added to the system. Thus, the speed and pressure of the air above a real wing in flight are not related by the Bernoulli principle. Also, descriptions of lift that evoke the Bernoulli principle depend on the shape of the wing. As already stated, the shape of the wing affects the efficiency and stall characteristics of the wing but not the lift. That is left to the angle of attack and speed.

MORE (Newton's Laws and Lift)
Source:
David Anderson,
Scott Eberhardt

Top of page


[HOME] [AVIATION] [How Airplanes fly] [History] [Records] [Humor] [News] [Photos] [Stories] [Stamps] [Sounds] [Movies] [HUMANS] [ORIGINS] [SCIENCE] [WEB LINKS] [SITE MAP] [CONTACT]